(Last updated 11/12/2019)

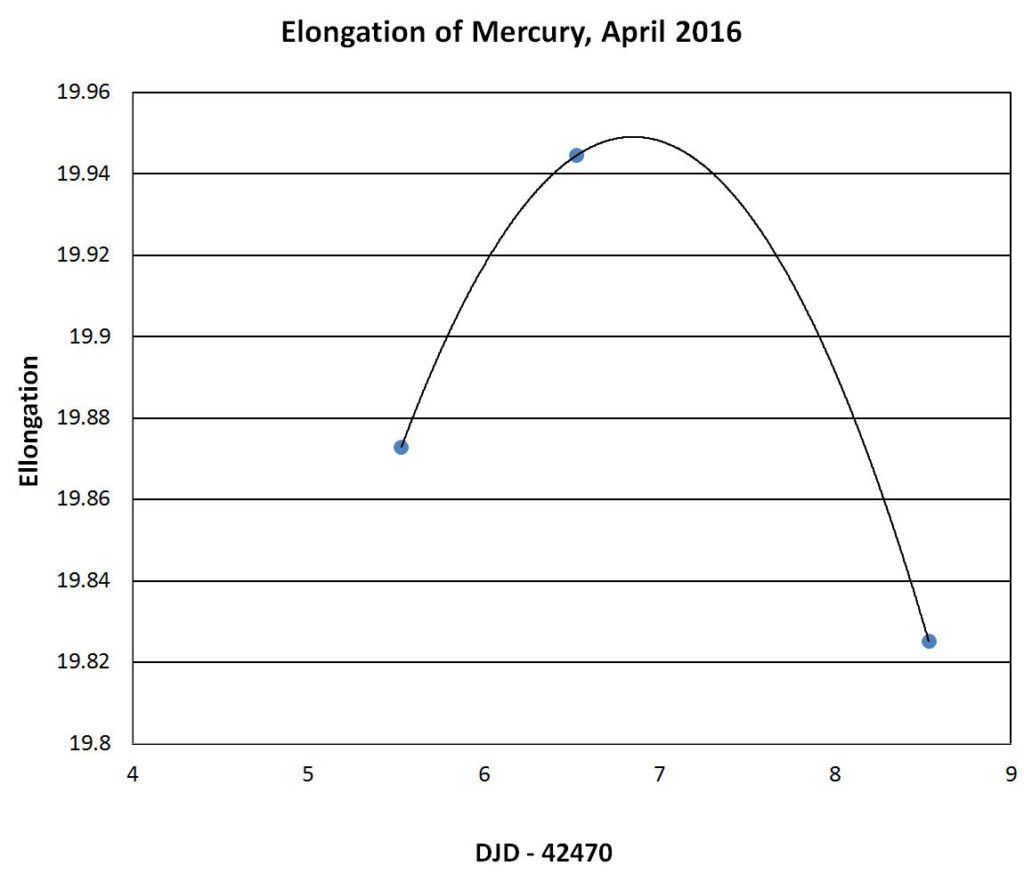
Mercury had a favorable eastern elongation in the Spring of 2016, as seen from the northern hemisphere and I was able for the first time to use my approach of taking star -field photographs to track it.  The graph shows the three points closest to maximum and from them I could locate the maximum to have occurred on 4/18/2016 at about 8:30 in the morning, Universal time.

In fact, since then I have followed Mercury through another eastern elongation, and I have two good photographic records of greatest western elongations. I can use the numbers from these to improve most of my values for the orbit parameters.  The two greatest western elongations are the easiest to use.  By chance, they seem both to have occurred at or close to perihelion.  The distances of Mercury from the Sun were 0.308 au for the September 2010 elongation and 0.307 for the September 2016 elongation.  The time interval between them is 2200.4 ± 1 days.  From the values that I already know I can see that this is 19 synodic years, so one synodic year is 115.8 ± 0.05 days.  Also, because the planet was close to perihelion the rule that the heliocentric longitude is 90° less than the ecliptic longitude should be very accurate.  The two heliocentric longitudes come out as 69.46° in 2010 and 77.95° in 2016.  Because the sidereal year is about 88 days, I can see that Mercury has made just over 25 revolutions around the Sun in this time interval, so the total angle it has turned through is (25×360 + 77.95 – 69.46)° or 25.024 revolutions, and the time for one revolution, which is the sidereal year, is 87.933 days.  I estimate the uncertainty as just below 0.040 days.  This converts into (0.2407 ± 0.0001) years.

I can get one more value, or at least an estimate.  My  value for the sidereal year corresponds to a semi-major axis of 0.387.  If I assume that the September 2016 distance is that for perihelion then it is a(1 – e), and I find an eccentricity for Mercury’s orbit of 0.207 ± 0.005.

May 9th 2016.  Finally!  I got to see a transit of Mercury, or at least half of it, for the first time.  Mercury is the lower dot.

I can use this photograph to get a somewhat rough value for the diameter of Mercury.  On the photograph the image of Mercury is 9 pixels across.   This corresponds to an angle of 12.3″ of arc.  From my measurements of the orbit, Mercury is about 0.45 au from the Sun and therefore 0.55 au from the Earth.  If it was moved away to be 1 au from the Earth its size would be 5 pixels.  The image of the Sun is 1395 pixels across, so the size of Mercury divided by the size of the Sun is 5/1395 = 3.6 × 10¯³.  My value for the diameter of the Sun is 1.389e6 kilometers, so the diameter of Mercury is just on 5000 km.  The uncertainty in the size of the image of Mercury is at least ±1 pixel and this translates into (0.0036 ± 0.0004) for the size of Mercury divided by the size of the Sun and (5000 ± 600) km for the diameter of Mercury.

I can use this value to make a guess at the mass of Mercury, just as I do for Venus.  If I assume that the density of Mercury is the same as the density of the Earth, I can use my values for the mass of the Earth and the diameters of Earth and Mercury to calculate a mass for Mercury of 3e23 kg.  To one significant figure this does agree with the handbook value, but it does depend on that assumption about the density.

I did also observe Mercury during the transit of November 11, 2019.  Apart from the pleasure of seeing a relatively rare phenomenon, which will not be visible again in this part of the world until 2049, I thought I might be able to get another value for its synodic period.  I have timings for the centers of the two transits that are accurate to a couple of hours, and I can divide the time interval between them by eleven, which it the number of inferior conjunctions Mercury has gone through in this time.  Alas, it didn’t work out particularly well.  The value I got was 116.5 days compared with my best number of 115.8 days.  This illustrates the idea I mentioned in my book, that the time it takes Mercury to complete a passage from one inferior conjunction to the next can very by several days.  I would need to wait for another transit a long time in the future to get a reliable value.